Divergence of Harmonic Series

Theorem

Despite the terms of the harmonic series trending to zero, the series itself diverges. This is a fact which is a natural follow on from the fact that the natural logarithm diverges.

Simply put, the harmonic series can be expressed as the sum of areas bounded below by the curve of \(\frac{1}{x}\):

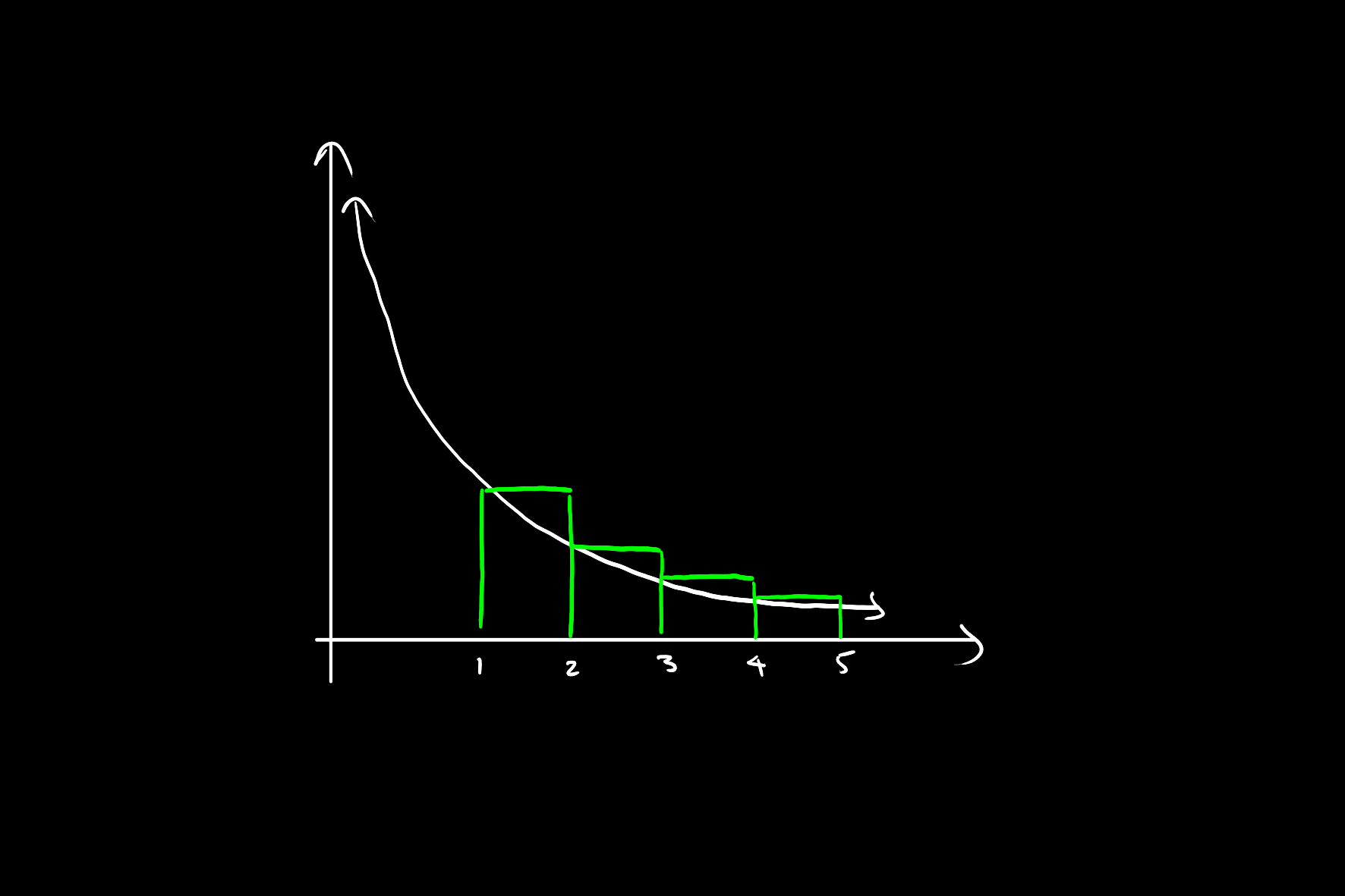
In the above, each green rectangle is of unit width, and the heights correspond with the values in the harmonic series. Therefore, the total area of such rectangles should be equal to the harmonic series. This however, is bounded below by the improper integral:

\[ \int_{1}^{\infty} \frac{1}{x} \,\mathrm{d}x = \lim_{x \to \infty} \ln(x)\]

which diverges.

However, it can also be proven more directly, and very cleanly, as follows:

Proof

Consider the following inequality for the harmonic series:

\[\begin{align*} \sum_{k = 1}^{\infty} \frac{1}{k} &= 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \dots \\ &> 1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{4} + \frac{1}{8} + \frac{1}{8} + \frac{1}{8} + \frac{1}{8} + \frac{1}{16} + \dots \\ \end{align*}\]

Specifically, we note that the right hand side of the above expression is smaller because the terms on the right are pairwise less than or equal to those on the left. That is, we replace all terms after \(\frac{1}{2}\) with \(\frac{1}{4}\) until we reach \(\frac{1}{4}\) in the original expression, and continue increasing the power of \(2\) on the denominator. Then, from \(\frac{1}{2^n}\) (non-inclusive) to \(\frac{1}{2^{n + 1}}\) (inclusive) we have exactly \(2^{n + 1} - 2^{n} = 2^{n}(2 - 1) = 2^n\) terms, and so when we add them up together each group of terms of this form is \(\frac{1}{2}\). Hence, we have:

\[\begin{align*} \sum_{k = 1}^{\infty} \frac{1}{k} &> 1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{4} + \frac{1}{8} + \frac{1}{8} + \frac{1}{8} + \frac{1}{8} + \frac{1}{16} + \dots \\ &= 1 + \frac{1}{2} + \frac{1}{2} + \frac{1}{2} + \dots \\ &= 1 + \sum_{k = 1}^{\infty} \frac{1}{2} \\ \end{align*}\]

and this sum clearly diverges.